Aksiyomlar Nedir
- “İki nokta bir ve bir tek doğruyu belirler” “Bir düzlemde verilen bir doğruya, bir noktadan bir ve bir tek paralel çizebiliriz”… İşte öklidyen geometri aksiyomları .“Sıfır bir tam sayıdır”, “Her sayının bir ve bir tek müteakipi vardır”… İşte doğal sayılar teorisiyle ilgili aksiyom örnekleri. Bu örnekleri çoğaltmamız mümkündür, çünkü her matematik teorisi, aksiyomlar sistemi üzerinde kurulmuştur.
- Matematikte aksiyomatik yöntem bir oyuna benzetilebilir. Santranç oyununda, başlangıçta bütün parçalar (taşlar) ve bu taşların oyunun başında nasıl yerleştirileceği, her taş için ilerleme yönleri belirlenmiştir. Bu veriler ile, oyuncular bir santranç partisi düzenleyerek, oyunu bu kurallar çerçevesinde dilediklerince sürdürürler. Aynı şekilde, bir matematik teorisinde de başlangıçta tüm matematiksel mevcutlar, bu mevcutlar arasındaki ilişkiler ve akıl muhakemelerinin düzenlenmelerini sağlayacak kurallar belirlenmiştir. Bu temel verilerle akıl muhakemeleri, teoremler, yeni mevcutlar, mevcutlar arasındaki yeni ilişkiler düzenlenebilir, yani teori genişletilebilir.
- Bu aksiyomatik metodun iki ayrı alanda nasıl kullanıldığını göreceğiz, geometride ve formel bir oyunda.
- Geometride başlangıçta verilen ve üzerinde çalışılacak olan nesneler 3 türlüdür; noktalar, doğrular ve düzlemler. Bu nesneler hakkında neler biliniyor ? Sadece aksiyomlarda verilen ve bunları birbirine bağlayan bir kaç bağıntı. Sıralandırma yapmaksızın, konunun başında belirttiğimiz iki aksiyoma ek olarak şu örnekleri de sıralayalım: “Aynı doğru üzerinde olmayan üç nokta bir düzlem belirtir” A, B, C, bir doğrunun üç noktasıysa ve B noktası A ile C arasında ise, B noktası aynı zamanda C ile A arasında’dır.” Temel veriler olan nesneler ve aksiyomlar ile bütün Euclidienne geometriyi oluşturabiliriz. Özellikle başka nesneler oluşturabilmemiz mümkündür.Mesela; üçgenler, açılar, çemberler, daireler, çok genler vs., Aynı zamanda da başlangıçtaki nesnelerin diğer özelliklerini de belirleyerek, yeni nesnelerin özelliklerini de ortaya çıkarabiliriz.
- Başlangıçtaki nesnelerin hiçbir tarifinin verilmediğini de belirtmeliyiz; somut, veya soyut işaretlerinin teorinin gelişmesinde önemi yoktur. Bu nesneler hakkında tek bildiklerimiz; aksiyom-larca açıklanan bazı bağıntılarıdır. Matematik bu nesnelerin türleriyle değil, bu nesneler arasındaki bağıntılarla ilgilenir. Aynı şekilde, satranç oyununda da taşların isminin veya şeklinin önemi yoktur, önemli olan taşların başlangıçtaki yerleri ve herbirinin ilerleme yönleridir.
- Şimdi de hiçbir anlamı olmayan nesnelerin kullanıldığı bir oyun düzenleyelim. Bunun için basit bir malzeme alalım; kırmızılar ve maviler. Bunlar ile bazdan müsait, bazdan ise müsait olmayan zincirler düzenlenebilir. Müsait zincirlerin oluşturulabilmesi için başlangıçta verilenler;
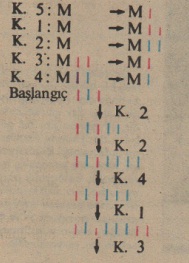
1) Temel zincirler (teorinin aksivomlan) Mesela I I I I I olası’dır.
2) Yeni zincirler oluşturulmasını sağlayan kurallar yukarki zincirle yapdır: dört örnek kural alalım: “M zinciri olası ise, buna iki kırmızı ekleverek yeni bir II olası zinciri elde ederiz.
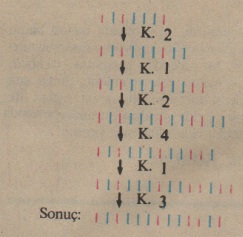
(l.kural)Veya iki mavi ekleyerek M I I elde ederiz. (2. kural). Olası zincir üç kırmızı ile bitiyorsa, en sonuncusunu kaldırabiliriz (3. kural), iki mavi ile., bittiğinde ise yine en sonuncusunu kaldırabiliriz (4. kural)
- II I’zincirine, kurallan uygulayarak, bu zincir elde edilebüir. I I I I I I I I
- Aksiyom olarak verilen üç zincirden başka zincirler de elde edebilir. Aynca Uk kurallardan, daha başka kurallar da elde etmek mümkündür. Mesela 1 ve 3 kurallarıyla 5 kuralı oluşturulabilir.
- Matematiksel bir teoriden, aksiyomatik bir izaha ulaşmak için etaplar halinde hareket edebilir.
- Uygulamasız kabul edilen özellikleri ve bağıntılar içeren bir envanter hazırlanır. Bunların anlatımları teorinin aksiyomunu oluşturacaktır.
- Aynca kendileri tanımlanamayan, başka tanımlamalara yarayan kelime ve simgelerin bir envanteri düzenlenir. Bu kelimelerin her zaman kullanılan öz anlamlarından soyutlaştırılması gerekir.
- Bu temel veriler açıkça belirlendikten sonra; teori oluşturulabilir: bunun için kullanılan simgeler arasında yeni bağıntılar oluşturul(temel bağıntılardan yararlanarak; başlangıçta verilen işaret ve simgeler kullanarak yenileri oluşturulur; bu yeni simgelerin özellikleri belirlenir… vs.
- Bilinen en eski aksiyomatik yapı girişimi; Euclide’u geometri üzerindeki eserlerinde bulunmuştur. (M.Ö. III. yüzyıl). Euclide’den sonra ancak XIX. yüzyılda matematikçiler yeni girişimlerde bulunmuşlardır: En önemlileri .XIX. yüzyılda Dedekind ve Peano‘nun aritmetik ve doğal sayılar üzerinde, Pash ve Hılbert‘in öklidyen geometri üzerinde yaptıklarını çalışmalardır.
 Geometri aksiyomu araştıran bazı matematikçder XIX. yüzyılda Euclide postulasını (veya aksiyomunu) bulmuşlardır: “Bir düzlemde, verilen doğrunun dışındaki bir noktadan, bu doğruya bir ve bir tek paralel çizebilir” Lobatchevsky bir başka aksiyomla yeni bir geometri kavramı elde etmiştir. “Bir düzlemde verilen doğrunun dışındaki bir noktadan, bu doğruya sonsuz sayıda paralel oluşturulabilir” Riemann ise bir başka aksiyomla yeni bir teori oluşturmuştur: “Bir düzlemde verilen doğrunun dışındaki bir noktadan bu doğruya hiçbir paralel çizilemez”. Bu teorilerin her biri, itirazsız geliştirilebilir.
Geometri aksiyomu araştıran bazı matematikçder XIX. yüzyılda Euclide postulasını (veya aksiyomunu) bulmuşlardır: “Bir düzlemde, verilen doğrunun dışındaki bir noktadan, bu doğruya bir ve bir tek paralel çizebilir” Lobatchevsky bir başka aksiyomla yeni bir geometri kavramı elde etmiştir. “Bir düzlemde verilen doğrunun dışındaki bir noktadan, bu doğruya sonsuz sayıda paralel oluşturulabilir” Riemann ise bir başka aksiyomla yeni bir teori oluşturmuştur: “Bir düzlemde verilen doğrunun dışındaki bir noktadan bu doğruya hiçbir paralel çizilemez”. Bu teorilerin her biri, itirazsız geliştirilebilir.
Şu Sayfamız Çok Beğenildi
Sayısal Mantık Çözümlü Sorular

Yorumlar
Henüz yorum yapılmamış.