• Çok eski, çağlardan beri, yoğun problemler matematikçileri birinci, ikinci dereceden eşitliklerin çözümüne götürmüştür. 19. yüzyıl başlarına kadar cebirsel eşitlikler cebirle uğraşanların tek meselesi olmuştur. Sayı kavramlarının gelişimi ve tam sayılar, negatif sayılar, rasyonel sayılar, kesirli sayılar, irrasyonel sayılar, sanal sayıların ortaya çıkmasına paralel olarak cebirsel eşitliklerin incelenmesinde de değişiklikler olmuştur.

• Mısırlılarda birinci dereceden eşitliklerle çözümlenen problemlere rastlanmıştır. Tarihî devrin başlangıcından 2000 yıl kadar öncelerde bu tip eşitliklerle, çözümleri ile birlikte karşılaşılmıştır. Daha sonraları Babilliler ve Yunanlılar çok bilinmiyenli birinci dereceden denklemlerin çözümünü gerçekleştirmişlerdir. Kullanılan metodlar basit olmayıp, sadece pozitif rasyonel sayılar çözüm olarak kabul ediliyordu. Hesaplamalarında en önce Çinliler negatif sayıları kullanmışlardır. Ortaçağda Araplarda birinci dereceden eşitlik sistemleri gelişmiş, ancak 18, yüzyılda cramer ile çok bilinmeyenli birinci dereceden denklem sistemlerinin çözümü gerçek anlamda ortaya çıkmıştır. 19. yüzyılda ise matematikçiler determinant ve matris hesaplamalarını kullanmaya başlamışlardır.

• Babillilerin o zamanlarda bile ikinci dereceden eşitliklerin çözümünü sağlayan metotları vardı. Yunanlılar bu tür eşitlikleri geometrik problemlerin çözümünde kullanıyorlardı. Ancak sadece pozitif rasyonel sayıları kullanıp,diskrimiriant dediğimiz değerin bazı hallerini bir kenara bırakmak zorunda kalıyorlardı.

• Üçüncü dereceden eşitlikler ise sadece özel hallerde Babillilerde kullanılıyordu, ancak genel bir teorileri yoktu. 16. yüzyılda İtalyan ekolünün matematikçileri bu probleme gerçek bir çözüm getirdiler. x3+px+q=0 şeklindeki eşitliğin çözümü ile başlayıp, sonuçlan şu şekilde belirttiler;

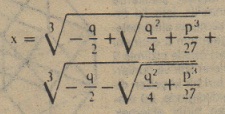
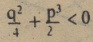•  Kabul ediliyordu, bu zorunluluk İtalyan matematikçileri karmaşık sayıların temeli olan sanal sayılan bulmaya itti.Dördüncü dereceden eşitliklerin çözümü de yine İtalyan matematikçiler tarafından gerçek­leştirilmiştir.

• 19. yüzyılda dördüncü dereceden daha  yüksek dereceli eşitliklerin çözümü için yapılan çalışmalar sonucunda daha genel ve daha soyut kavramlar olan grup, cisim, halka sonuçla­rına varılmıştır.

• Bir x bilinmeyenli cebirsel eşitlik P(x)=0 şeklinde yazılabilir. Burada P(x) katsayıları reel sayılar olan bir polinomu ifade etmektedir. Eşitliğin derecesi olarak, P(x) polinomunun derecesi kabul edilebilir. Gerçel veya karmaşık sayı olabilen a, x yerine a konduğunda, sıfıra eşitliği gerçekleşiyorsa, bu eşitliğin köküdür denir.

• n dereceden bir eşitliğin n tane gerçel veya karmaşık olabilen kökü vardır. Karmaşık köklerin sayısı her zaman çifttir. Yani eğer eşitliğin derecesi tek sayıysa, en azından bir tane gerçel kökü çözüm olarak kabul edecektir. Aynı şekilde ikinci dereceden eşitliklerin ya iki farkı gerçel kökü  veya birbirine eşit iki gerçel kökü  ya da iki karmaşık sayı kökü vardır. Üçüncü dereceden bir eşitliğin ise bir gerçel kökü ve gerçel veya karmaşık olabilen iki kökü daha vardır.

• Eğer a P(x)= 0 eşitliğinin kökü ise ve eğer P(a)=0 ise, P(x) polinomu x-a ile bölünebilir denir. Başka bir deyişle, P(x) polinomunun derecesinden 1 eksik dereceli Q(x) polinomu vardır ve bu P(x)=(x-a) Q(x) şeklinde yazılır. Bunun sonucunda, eğer a,, a 2, a 3…, a„ P(x)=0 eşitliğinin kökleri ise P(x) polinomu birinci dereceden çarpanların çarpımı şeklinde yazılabilir:

P(xHx-a,) (x-a2) (x-a3)… (x-a„),

P(x) polinomunun katsayıları eşitliğinden basit köklerinin ifadesidir. İkinci dereceden

a x 2+ b x +c=0

denkleminde x, ve x2 kökler ise, şunlar yazılabilir.

b x,+x2=-— (köklerin toplamı)

c ve x, x2= ~ (köklerin çarpımı)

Bu sonuçlan uzatmak ve genelleştirmek mümkündür.

• Bir cebirsel eşitliğin kesin veya yaklaşık sayısal değerinin belirlenmesi hesaplama veya grafik yolla yapılabilir. Bu kavramlar ordunatörler yardımıyla daha etkili hale getirilebilir. 1,2,3,4. dereceden eşitliklerin çözümü cebirsel olarak hesaplanır. Galois adlı matematikçi daha yüksek dereceli eşitliklerin çözümünü gerçekleyebilmek amacı ile “yerine koyma metodunu geliştirmiştir.