• Frekansı “temel” sayılan bir frekansın tam katlarından biri olan sinizoidal hareket harmonik olarak adlandırılır ve akustik, optik,radyo dalgalan gibi çeşitli alanlarda kullanılır. Harmonikte temel hareket titreşimdir.

• Titreşimin ne olduğunu açıklayabilmek için ucunda bir ağırlık asılı olan sarkaç örneğini inceleyelim. Bu ağırlık aşağıya doğru çekilip, sonra bırakıldığında ağırlık otomatik olarak yukarı çıkacaktır ve denge durumu etrafında gidiş geliş hareketlerine devam edecektir. Bazı duvar saatlerinde görebildiğimiz bu tekrarlanan hareket titreşim olarak adlandırılır.

• Mekanik titreşim örnekleri çok sayıdadır: Makinelerin titreşimleri, gitarın titreşen teli, bir tüp içindeki titreşen hava kolonu (Bu hava kolonu hızlı basınç değişimleri gösterir). Bu titreşimlerirı bazıları bir ses üretir, bazıları ise madde içindeki moleküllerin titreşimleri gibi görünmezdir.

• Sallanan bir elektrik devresinde, elektrik yüklerinin hareketi magnetik ve elektrik alan titreşimleri üretir. Bir titreşim hava gibi bir ortamda yayıldığında, dalgalardan söz edilir. Bu dalgalar elektromagnetik olabildiği gibi, mekanik de olabilir.

• Tekrar sarkaç örneğini ele aldığımızda belirli bir durum çevresindeki ağırlığın;,tam bir gidiş geliş zamanı her zaman aynıdır; buna  hareketin T periyodu denir. Periyod; titreşen bir cismin tam bir titreşim yapması için geçen zaman aralığıdır. Hertz birimli N frekansı, periyodun tersidir. Yani 1000 Hz.’lik bir sesin periyodu 0,001 saniyedir. Bir titreşimin genliği ise maksimum yer değiştirmedir. (Harmonik hareket yapan bir cismin herhangi bir andaki yer değiştirmesi, o anda orta noktadan olan uzaklığıdır).

• Titreşim hareketleri az veya çok komplike olabilir. En basit temel hareket “harmonik titreşim” olarak adlandırılır. Bu, sabit genlik ve frekansta eşitliği zamanın sinuzoidal bir fonksiyo¬nu olan bir titreşimdir. Mekanik bir sistemin zayıf genlikli titreşimleri harmonik titreşim olarak ele alınabilir.

• Kompleks bir periyodik titreşim, harmonik titreşimler toplamı olarak gösterilebilir. Buna harmonik analiz adı verilir. Matematik olarak FN fonksiyonu; frekansları başlangıç frekansının katlan olan sinizoidal fonksiyonlar toplamının, titreşimi olarak ifade edilir, fonksiyonun Fourier serisine göre açılımı gerçekleştirilir.

FN = f N + f 2N+ f3N + f4n + —

• Frekansı başlangıç frekansına eşit olan kısmi titreşim temel titreşimdir (ana ses).Diğer f2N, f3N… kısmî titreşimleri 2,3… derecelerden harmonik hareketlerdir. Fourier serisinin katsayılarının araştınlması matematik problemidir. Ancak bir fizik sisteminde bu katsayılar (harmonik hareketlerin frekansları ve genlikleri) harmonik analizörler tarafından ölçülebilir; bunlar mekanikte frekans metreler, elektrikte osiloskoplardır.

• Örnek olarak kompleks bir müzikal sesin analizini alalım: İlk anlarda, bir mikrofon ses titreşimlerini elektrik titreşimler haline dönüştürür (harmonik hareketle aynı yapıda olan). Elektrik titreşimleri osiloskoplar yardımı ile analiz edilir.

• Bir analizin sonuçları bir tayf şeklinde gösterilir. Absise; harmonik hareketlerin frekansları; ordinata ise genlikleri yazılır

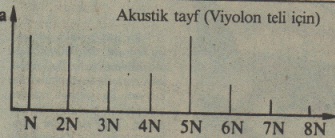
• Akustikte bir sesin müzikal tını kendisini oluşturan harmonik hareketlerin rölatif şiddet ve sayılarına bağlıdır. Şu veya bu armoni kuvvetlen-dirilebilir; bir gitarın 2. dereceden akordunun oluşturulması kolaydır. Ayrıca bir sesin birbirini takip eden harmonilerinin sentezi de gerçekleştirilebilir. Bu elektronik müzik aletlerinin bobininde sinizoidal elektriksel titreşimler oluşturulacak armonilere tekabül ederler.

• Bir radyo anteni istenmeyen harmonilerle kaza ile uyarılabilir. Bunu önlemek amacı ile armonik filtreler kullanılır; bunlar radyo dalgasının ana bileşeninin armonilerini antene ulaşmadan ayırırlar.