İntegral
- İntegral kavramı; alan ölçümlerinin gerekliliğine bağımlıdır. Bu gereklilik, çok uzun zaman önce ortaya çıkmıştır. Yunanlılar çok önceden beri önemli alan kavramlarını tanıyorlardı (üçgen, dikdörtgen vs.).Daha karmaşık yüzey hesaplamalarıyla karşılaştıklarında, bu karmaşık yüzeyi çeşitli bilinen alanlara ayırıp, bu alanlan toplayarak yaklaşık sonuca varıyorlardı.
- M.Ö. IV. yüzyılda Eudoxe bu konuda çalışmalarda bulunmuştur. XIX. y yılda Riemann tarafından açıklanan integral hesaplama kuralları Eudoxe‘un çalışmalarının benzeridir. Bu hesap türü, özellikle fizikte geniş alanlarda kullanılmaktadır.
- [a,b] aralığında sürekli pozitif bir f fonksiyonu düşünelim, bu fonksiyonun eğrisini C ile gösterelim. Bu C eğrisi ile Ox ekseni ve x=a x=b eşitliğindeki doğrular arasında kalan alanı hesap lamak isteyelim. Riemann bu alanı n kısmi aralığa bölmeyi önermiş ve bu aralıkların eşit olmayabileceğini vurgulamıştır. Bu aralıkları alanları,tabanı xi – xi-1’in yükseklik f(ci) ile çarpımı olacak şekilde dikdörtgenler haline dönüştürmüştür. (i=seçilen kısmî aralığın numarası. Ci=xi, xi-1 aralığının bir noktası) Aranan alan o halde, kısmî aralıkların kalınlığı sıfıra yaklaştığında limit olacaktır.
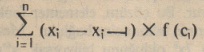
formülü “Riemann toplamı” olarak adlandınlır. Üsteki şekil Riemann teoreminin n eşit kalınlıkta kısmî aralıklar ile uygulanmış şeklidir. Bu şekle ait Riemann formülü,
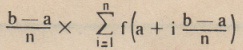
Bütün bu toplamlann limiti mevcutsa, f integre edilebilir denir ve
![]()
Burada dx sonsuz küçük kısmî aralığın kalınlığını belirten bir semboldür.
İntervalin uçlarından birine x değişkeni yerleştirildiğinde; (,a,xi aralığı olacaktır.) İlkel fonksiyondan bahsedilecektir ve denklem;
![]()
Bir f fonksiyonun belirsiz integrali, veya ilkel fonksiyonun belirsiz integrali, veya ilkel fonksiyonu; türevi f(t) olan bütün f(t) fonksiyonlarını kapsayacaktır.
![]()
Bu eşitliğin çözümü; integral hesabın amacını oluşturur. Bu çözüm, elementer fonksiyonların türevlerinin bilinmesine bağlıdır. Mesela x”nin türevinin 7x6 olduğunu biliyorsak, x6‘nın ilkel fonksiyonu
![]()


Yorumlar
Henüz yorum yapılmamış.