Sayım (Sıralama)
- Bir kümenin elemanlarını sayılamak, bir envanter oluşturmak demektir. İki hatadan sakınılmalıdır: Bazı elemanları unutmak veya aynı elemanları bir kaç defa tekrarlamak
- Bir kitapçının 50 defteri var. Bu defterlerden 30 tanesinin yeşil, geri kalanının kırmızı olduğunu ve 25 tanesinin 100 sayfalı, diğerlerinin 200 sayfalı olduğunu biliyor. Bu verilerden faydalanarak diğer ihtimaller hesaplanabilir. Mesela, 200 sayfalı kaç yeşil defterin olduğu, 200 sayfalı kaç kırmızı defterin olduğu vs… Bu tür örneklerde, A ve B iki kümeyse, kardinal toplama işlemi uygulanır.

- 1,2,3 olarak numaraladığınız üç topu a,b,c,d çekmecelerine yerleştirmek isteyelim. Bu düzenlemeyi kaç değişik şekilde yapabiliriz? Her çekmeceye istediğimiz kadar top koyma imkânımız var. Cevap 43 farklı şekilde olmalıdır. Çünkü 1 topu 4 değişik şekilde yerleştirebilir, 1 nolu topun yerine bakılmaksızın 2 nolu top yine 4 değişik şekilde yerleştirilebilir vs…
- Üç elemanlı bir kümenin, dört elemanlı bir kümeye uygulanma sayısı yine 43 yani 64’tür. Bu sonuç genelleştirilerek n elemanlı bir kümenin, p elemanlı bir kümeye uygulanma sayısı ”p” olarak ifade edilir (bu bir eksponansiyeldir).
- Şimdi de üç topun, her çekmecede en fazla bir top olacak şekilde beş çekmeceye yerleştirilmesini düşünelim. O durumda 5x4x3 değişik yerleşim biçimi gerçekleşecektir. Çünkü 1 no’lu top bir çekmeceyi işgal ettiğinde, 2 no’lu top yalnızca boş kalan diğer dört çekmeceden birine yerleşebilecektir. Aynı şekilde üç elemanlı bir kümenin, beş elemanlı bir kümeye bire bir örten değil, fonksiyon sayısı 5x4x3 olacaktır.
- Birebir örten değil fonksiyonlara bu sonuç genelleştirildiğinde, n elemanlı bir kümenin, p elemanlı bir kümeye birebir örten değil fonksiyon sayısı, “p(p~l)(p-2) (p-n+1)” n^p olarak gösterilir.
- Bu ifadeyi aynı sayıda eleman içeren kümelerin birebir örten hallerine de uygulayabiliriz, n eleman sayısı ise n=p yazılır. Birebir örten fonksiyon sayısı “n(n-l)(n-2)( ) 2-1” olarak gösterilir. Bu da n! olarak ifade edilir.
- Bir kümenin kaç alt kümesi olacaktır. a,b,c üç elemanlı bir kümenin sekiz alt kümesi olacaktır. Bunlar (0), (a), (b), (c), (a,b), (a,c), (b,c) ve (a,b,c)‘dir. 3 elemanlı bir kümeden 4 elemanlı bir kümenin alt kümelerine geçiş 2 katını almakla gerçekleştirilir. Dört elemanh bir kümenin 16 alt kümesi olacaktır. Genel olarak ifade edildiğinde, n elemanh bir kümenin 2″ adet alt kümesi olacaktır.
- p ve p olarak alman n nesnenin kombinezonu, veya p elemanlı alt kümeler sayısı (n elemanlı bir kümede) farklı olacaktır. Bu sayı C(n,p) olsun. Bunu formül ile göstermek çok uzundur.
- C(n,p)=C(n-l,p)+C(n-l, p-1)... Bu ifadeyle, bir öncekiler ile bu sayılardan birinin değerini hesaplayabilmek mümkündür. Bu formül yardımı ile bu sayıların değerlerini gösteren tablolar düzenlemek mümkündür. Bu tablo bir üçgen şeklinde olacağından “Pascal Üçgeni” olarak adlandırılır, n elemanlı bir kümenin, p elemanlı alt küme sayısı C(n,p) olarak ifade edilir, n yatay sıra üzerinde, p dikey sıra üzerinde gösterilir.
- Bu sayıların her birinin diğerlerinden bağımsız olarak hesaplanmasını sağlayan bir diğer formül:
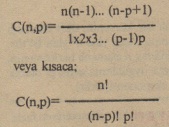
- Sayılama örneklerini çoğaltmak mümkündür. Her alanda bu problemler karşımıza çıkabilir. Bu tür problemler özellikle 17. yüzyıldan itibaren incelenmeye başlanmış, matematiğin yeni bir dalını oluşturmuştur, temel sayma problemleri adını almıştır.
Şu Sayfamız Çok Beğenildi
Sayısal Mantık Çözümlü Sorular

Yorumlar
Henüz yorum yapılmamış.