Tasarı Geometri
- Matematikçi Monge‘un ifade ettiği tasarı geometri üç boyutlu, öklidiyen, afin E uzayının bir bölümünün gösteriliş şeklidir. Bu gösteriliş p ve p ve p1 gibi izdüşümlerle gerçekleştirilir.
- Bunlar Oxy ve Oyz gibi dik iki düzlemde söz konusudur ve izdüşümün (H) yatay düzlem ve (F) ön taraf düzlemi olarak adlandırılır, Oy etrafında T yer çizgisi ile belirlenir. Profil düzlemi Oxz düzleminde p1 iz düşümü bazı durumlarda oldukça önemlidir.
- (x,y,z) koordinatlı bir M noktası 1. ve 2. figürlerde görüldüğü gibi (m,m) keskiyle belirlenir. Bu kesit F’nin H boyunca katlanması ile elde edilir. Yer çizgisini ju’de kesen mm rapel çizgisi ile şu bağlantılar elde edilir:
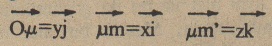
- Uzayın bir doğrusu (d,d) kesiti ile gösterilir, d ve d, H ve F üzerindeki izdüşümleridir. Bu şekilde dikey, profil, yatay doğrular elde edilir. Aynı şekilde düzlemler ve uzayın bütün noktalar kümesi gösterilebilir.
- Bu tür bir gösteriliş, şeklin D düzleminde E uzayının gerçek bir gösterilişidir. E’nin her figürünün D’de tek bir görüntüsü vardır ve ters olarak da D’deki her olası gösterilişe E’nin bir tek figürü tekabül eder.
- Bu yüzden, tasan geometri endüstriyel resmin prensibini oluşturur. Endüstriyel resim uzayın hacimler düzlemi içinde gösteriliş tarzlarını ifade eder. Uzay geometri problemlerinin grafik çözümlerini gerçekleştirilmesini sağlar; düzlem kesitler veya koni, silindir, küre gibi şekillerin kesişimleri gibi. Tasan geometrinin bakırcılıkta, ve mekanikte saç kesimlerinde çeşitli kullanım alanlan vardır. Baca borularının eklenmesinde, düz saçların kesilip tencere yapılmasında, denizciliğe ait yapımlarda hep tasan geometriden yararlanılır.
- G. Monge (1746~ 1818) tasan geometriye ait su tanımı yapmıştır. Bu sanatın ilci temel nesnesi vardır: Birincisi üç boyutlu olan şekillerin iki boyutlu resimler halinde doğrulukla gösterilebilmesidir. ikincisi ise, cisimlerin karşılıklı pozisyon ve şekillerine göre doğru olarak tasarlanabilmesidir.
Şu Sayfamız Çok Beğenildi
8. Sınıf Türkçe TEOG Çıkmış Sorular Ve Denemeler

Yorumlar
Henüz yorum yapılmamış.