Trigonometri
- Matematiğin açılan inceleyen bölümü trigonometriyi oluşturur. Trigonometri; açılar ile gerçel sayılan bağdaştırarak açı ölçülerini bildirir. Aynca açılar ve uzunluklar arasında da bağıntılar gerçekleştirir, üçgen örneğinde açılar ve kenar uzunluklan arasındaki bağıntıda olduğu gibi. Fizikte olduğu gibi, diğer bilim dallannda da periyodüobir çok olayın incelenmesinde trigono-metriden yararlandır. Uçak, gemi yapımlarında, yıldızların görülmesinde trigonometrinin gereği kaçınılmazdır.
- Herhangi bir düzlemde alınan, aynı bir noktadan çıkan iki yarım doğru bir açı oluşturur. Bu açıyı (0x, Oy) olarak gösterelim. Ve saat ibresinin ters yönünde bir dönme yönü seçelim.
- İki açının eşdeğerli olmaları, çevrel çemberin çevresinde yer değiştirme işlemi (translasyon veya rotasyon) uygulanarak bir yerde karşılaşmaları sonucu meydana gelir. Eşdeğerlilik. kaçınılmaz bir sonuçtur; çünkü aynı ölçüdeki açıların kümesinin saptanmasına yarar. Aynı ölçüdeki acılar eşdeğerlidir.
- Trigonometrik çember; yarı çapın birim uzunluk olarak belirlendiği, O merkezli yönlü bir çemberdir. Birbirlerine dik olan Ox ve Oy eksenlerini çizelim. Ox ekseni çemberi A, A’ noktalarında; Oy ekseni de çemberi B, B’ noktalarında kessin. Her x açısına, trigonometrik çemberin bir M noktası karşılık gelecektir. M noktasını; (OA, AM) açısı dikkate alınan açıya eşdeğer bir açı teşkil edecek şekilde alalım.
- M noktasının absisi (Birinci bileşeni) açının kosinüsüdür.
- M noktasının ordinatı (ikinci bileşeni) açının sinüsüdür.
- Sinüsün, kosinüse oranı açının tanjant değerini verir.
- Seçilen birim sistemine göre (radyan, derece, grad) her gerçel sayıya bir ve bir tek açı tekabül edecektir. Ancak, ters işlemde, trigonometrik çemberin her açısına sonsuz sayı tekabül eder, bu sayılar çemberin bir tam turuna eşit sayı kadar farklılık gösterecektir, yani 2 radyan, veya 360°, veya 400 grad kadar. Güncel hesaplamalarda belirli açılar için düzenlenmiş trigonometrik cetvel değerleri ezberde tutulmalıdır.
- Herhangi bir a açısı için aşağıdaki bağıntılar kaçınılmazdır:
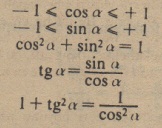
Her t sayısına karşılık! olan radyan ile ifade edilmiş açılann ölçülerini gözönüne alalım. Bu ölçüye bir ve bir tek açı karşılık gelecektir, bunu da cos t olarak gösterelim. Bu ifadeyi sayısal bir fonksiyonla da gösterebiliriz. Bir t sayısına, bir cos+ sayısı karşılıktır. Aynı şekilde bu açı için sinüs t ve tanjant t değerlerini de saptayabiliriz. Kosinus fonksiyonun özellikleri
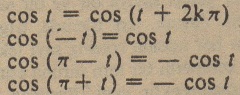
Sinüs fonksiyonunun özellikleri:
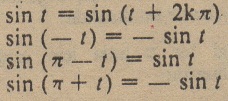
Tanjant fonksiyonunun özellekleri:
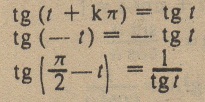
Ayrıca aşağıdaki bağıntılar da yazılabilir:
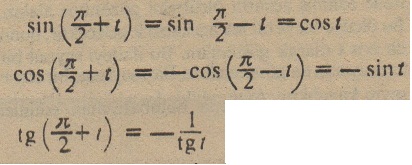
Tanjant fonksiyonunun tersi olan kotanjant fonksiyonunu da tanımlamak mümkündür. Bu fonksiyonun özellikleri;
cotg t=1/tg t
Grafikler üzerinde de görebileceğimiz gibi trigonometrik fonksiyonların değişimleri periyodiktir. Dalgalar gibi titreşimli olayların incelenmesinde bu fonksiyonlardan yararlanılır.
BAZI FORMÜLLER




Yorumlar
Henüz yorum yapılmamış.